Extrempunkte der Schar
Inhaltsverzeichnis
\(\\\)
Werte von a
Für die Extremstellen von \(f_a\) gilt
\( \quad \begin{array}{ r c l l } a \cdot x^2 & = & 1 & \bigl| \; : a \\[8pt] x^2 & = & \frac{1}{a} & \bigl| \; \sqrt{\dots} \\[8pt] x_1 & = & \sqrt{\frac{1}{a}} \\[8pt] x_2 & = & -\sqrt{\frac{1}{a}} \\ \end{array} \)
\(\\\)
Für die Extremstellen \(x_1\) und \(x_2\) gilt nun, dass \(a\) weder Null noch negativ sein kann. Daraus folgen die \(a\)-Werte bei
\(\\\)
-
Gruppe \(\textrm{I}\) mit \(\{a|a > 0, a \in \mathbb{R} \}\), denn Gruppe \(\textrm{I}\) beinhaltet alle Graphen der Schar mit zwei Extrempunkten.
-
Gruppe \(\textrm{II} \;\) mit \(\; \{ a|a \leq 0, a \in \mathbb{R} \}\), denn Gruppe \(\textrm{II}\) beinhaltet alle Graphen der Schar ohne Extrempunkte.
\(\\[2em]\)
Ortsgerade der Extrempunkte
Zunächst brauchen wir die \(y\)-Werte der Extrempunkte und setzen die \(x\)-Werte bei
\( \quad f_a(x) \; = \; x \cdot e^{-\frac{1}{2}a \cdot x^2 + \frac{1}{2}} \)
\(\\\)
ein.
\( \quad \begin{array}{ r c l } f_a\left(\sqrt{\frac{1}{a}}\right) & = & \sqrt{\frac{1}{a}} \cdot e^{-\frac{1}{2} \cdot a \cdot \left(\sqrt{\frac{1}{a}}\right)^2 + \frac{1}{2}} \\[8pt] & = & \sqrt{\frac{1}{a}} \cdot e^{-\frac{1}{2} \cdot a \cdot \frac{1}{a} + \frac{1}{2}} \\[8pt] & = & \sqrt{\frac{1}{a}} \cdot e^{-\frac{1}{2} + \frac{1}{2}} \\[8pt] & = & \sqrt{\frac{1}{a}} \cdot e^0 \\[8pt] & = & \sqrt{\frac{1}{a}} \\[18pt] f_a\left(-\sqrt{\frac{1}{a}}\right) & = & -\sqrt{\frac{1}{a}} \cdot e^{-\frac{1}{2} \cdot a \cdot \left(-\sqrt{\frac{1}{a}}\right)^2 + \frac{1}{2}} \\[8pt] & = & -\sqrt{\frac{1}{a}} \cdot e^{-\frac{1}{2} \cdot a \cdot \frac{1}{a} + \frac{1}{2}} \\[8pt] & = & -\sqrt{\frac{1}{a}} \cdot e^{-\frac{1}{2} + \frac{1}{2}} \\[8pt] & = & -\sqrt{\frac{1}{a}} \cdot e^0 \\[8pt] & = & -\sqrt{\frac{1}{a}} \\ \end{array} \)
\(\\\)
Als nächstes formen wir
\( \quad a \cdot x^2 \; = \; 1 \\ \)
\(\\\)
nach \(a\) um.
\( \quad \begin{array}{ r c l l } a \cdot x^2 & = & 1 & \bigl| \; : x^2 \\[6pt] a & = & \frac{1}{x^2} \\ \end{array} \)
\(\\\)
Die Ortskurve der Extrempunkte, die sich später als Gerade herausstellt, nennen wir \(y\) mit
\( \quad y\left(\sqrt{\frac{1}{a}}\right) \; = \; \sqrt{\frac{1}{a}} \\ \)
\(\\\)
Das \(y(-a)\) brauchen wir wegen der Punktsymmetrie nicht überprüfen. Denn \(f_a\) mit
\( \quad f_a(x) \; = \; x \cdot e^{-\frac{1}{2}a \cdot x^2 + \frac{1}{2}} \)
\(\\\)
ist ebenso wie \(f\) mit
\( \quad f(x) \; = \; x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} \)
\(\\\)
punktsymmetrisch. Das \(a\) in \(f_a\) beeinflußt die Punktsymmetrie nicht. Nun setzen wir \(a\) in \(y\) ein und vereinfachen die Gleichung.
\( \quad \begin{array}{ r c l } \displaystyle{y\left(\sqrt{\frac{1}{\frac{1}{x^2}}}\right)} & = & \displaystyle{ \sqrt{\frac{1}{\frac{1}{x^2}}} \cdot e^{-\frac{1}{2} \cdot \frac{1}{x^2} \cdot \left(\sqrt{\frac{1}{\frac{1}{x^2}}}\right)^2 + \frac{1}{2}}} \\[10pt] \displaystyle{y\left(\sqrt{x^2}\right)} & = & \displaystyle{ \sqrt{x^2} \cdot e^{-\frac{1}{2} \cdot \frac{1}{x^2} \cdot \left(\sqrt{x^2}\right)^2 + \frac{1}{2}}} \\[6pt] \displaystyle{y(x)} & = & \displaystyle{x \cdot e^{-\frac{1}{2} \cdot \frac{1}{x^2} \cdot x^2 + \frac{1}{2}}} \\[6pt] \displaystyle{y(x)} & = & \displaystyle{x \cdot e^{-\frac{1}{2} + \frac{1}{2}}} \\[6pt] \displaystyle{y(x)} & = & \displaystyle{x \cdot e^0} \\[6pt] \displaystyle{y(x)} & = & \displaystyle{x} \\[6pt] \end{array} \)
\(\\\)
Damit ist die Ortsgerade \(y=x\) bestätigt.
\(\\[2em]\)
Viereck
Das Viereck mit den angegebenen Punkten
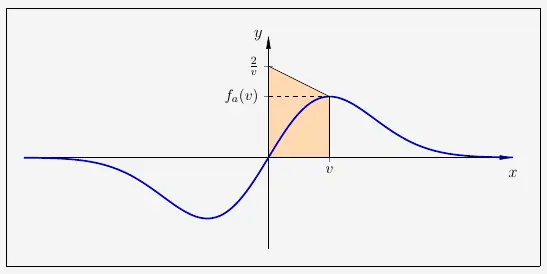
stellt stets ein Trapez dar, wobei die exakte Form abhängig von der Größe des Vierecks ist. Die Fläche eines Trapezes
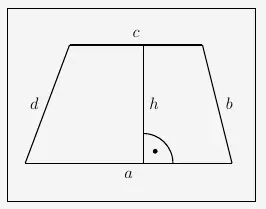
wird berechnet mit
\( \quad A \; = \; \frac{a+c}{2} \cdot h \)
\(\\\)
Das zu berechnende Trapez ist hochkant dargestellt und muss einmal gedreht werden. Alle Werte dann eingesetzt ergibt dann
\( \quad \begin{array}{ r c l } 49 & = & \frac{\frac{2}{v}+f_a(v)}{2} \cdot v \\ \end{array} \)
\(\\\)
Wie bereits fest gestellt haben die Extrempunkte die Werte \(\left(\sqrt{\tfrac{1}{a}} \, \biggl| \sqrt{\tfrac{1}{a}}\right)\) und \(\left(-\sqrt{\tfrac{1}{a}} \, \biggl| -\sqrt{\tfrac{1}{a}}\right)\). Der Hochpunkt muss der Extrempunkt mit dem positiven \(y\)-Wert sein. Also ist der Hochpunkt \(H\left(\sqrt{\tfrac{1}{a}} \, \biggl| \sqrt{\tfrac{1}{a}}\right)\) und der Tiefpunkt \(T\left(-\sqrt{\tfrac{1}{a}} \, \biggl| -\sqrt{\tfrac{1}{a}}\right)\). Den Hochpunkt nun in die Gleichung eingesetzt ergibt
\(\\\)
\( \quad \begin{array}{ r c l l } 49 & = & \frac{\frac{2}{\sqrt{\tfrac{1}{a}}}+\sqrt{\tfrac{1}{a}}}{2} \cdot \sqrt{\tfrac{1}{a}} & \biggl| \; \cdot 2\\[8pt] 98 & = & \left(\frac{2}{\sqrt{\tfrac{1}{a}}}+\sqrt{\tfrac{1}{a}} \right) \cdot \sqrt{\tfrac{1}{a}} \\[10pt] 98 & = & \frac{2 \cdot \sqrt{\tfrac{1}{a}}}{\sqrt{\tfrac{1}{a}}}+\sqrt{\tfrac{1}{a}} \cdot \sqrt{\tfrac{1}{a}} \\[8pt] 98 & = & 2 + \left( \sqrt{\tfrac{1}{a}} \right)^2 & \Bigl| \; -2\\[8pt] 96 & = & \tfrac{1}{a} & \bigl| \; \cdot a \\[8pt] 96a & = & 1 & \bigl| \; : 96 \\[6pt] a & = & \frac{1}{96} \\ \end{array} \)
\(\\\)